Artificial Intelligence Question Bank with Answers : part 3

Artificial Intelligence Question Bank with Answers: part 1 link click here

Artificial Intelligence Question Bank with Answers: part 2 link click here

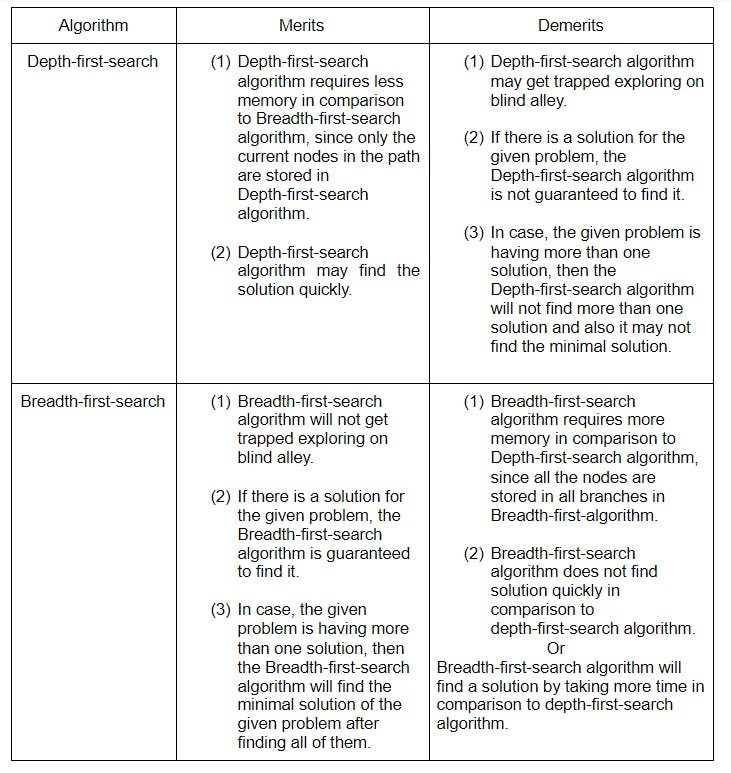
Q20. Write the merits and demerits of the Breadth-first-search algorithm and depth-first-search algorithm. Or What are the differences between the breadth-first-search algorithm and the depth-first-search algorithm?

Q20.Answer:

21) Write the steps of a simple Hill Climbing algorithm.

21.Answer:

22) Write the steps of a steepest-Ascent Hill climbing algorithm or gradient search algorithm.

Q22.Answer:

23) Explain the problem of (i) Local maximum, (ii) plateau and (iii) a ridge. And also explain how to overcome these problems.

23.Answer:

25. Write the steps of an algorithm which combines the merits of breadth-first search and depth-first search algorithm:

25.Answer:

27. Define (i) OR-graph, (ii)AND-OR graph. Explain with examples.

27.Answer:

(i) OR-graph:

OPEN - Nodes that have been generated and had the heuristic function applied to this but which have not yet been examined.

CLOSED - Nodes that have already been examined. We need to keep these nodes in memory, if we want to search a graph rather than a tree, since whenever a new node is generated, we need to check whether it has been generated before.

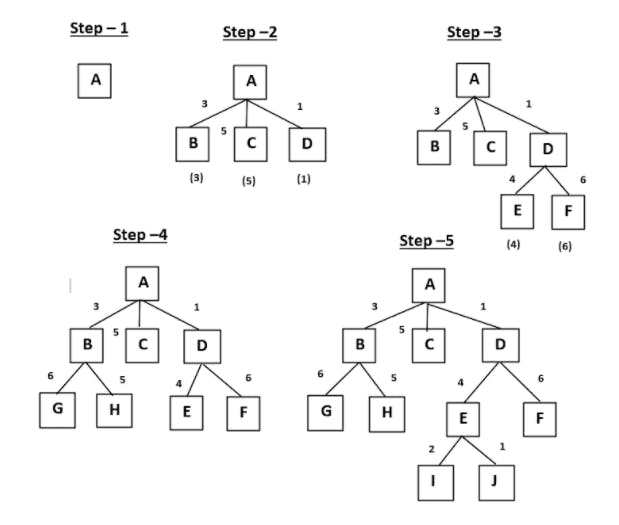
(ii) AND-OR graph:

The AND-OR graph (or tree) is useful for representing the solution of problems that can be solved by decomposing them into a set of smaller problems, all of which must then be solved.

This decomposition or reduction, generates arcs that we call AND arcs. One AND arc may point to any numbers of successor nodes, all of which must be solved in order for the arc to point to a solution.

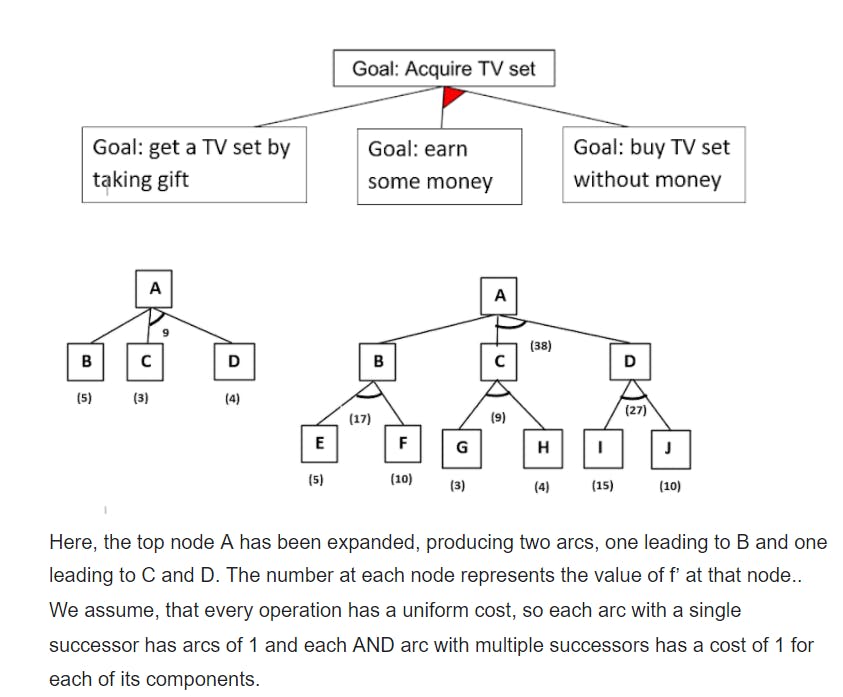
28)Define FUTILITY. Write the steps of the problem reduction algorithm.

Q28.Answer

FUTILITY

In order to describe an algorithm for searching an AND-Or graph, we need to exploit a value that we call FUTILITY. If the estimated cost of a solution becomes greater than FUTILITY then we abandon the search. FUTILITY should be chosen to correspond to a threshold such that any solution with a cost above it is too expensive to be practical, even if it could ever be found.

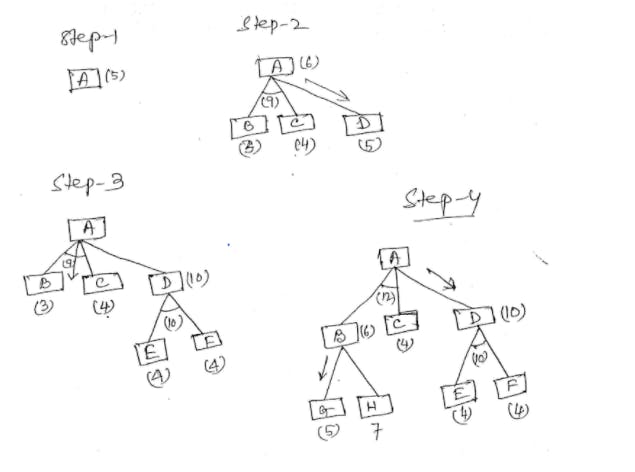
Algorithm : Problem Reduction

Initialize the graph to the starting node. Loop until the starting node is labeled SOLVED or until its cost goes above FUTILITY:

(a) Traverse the graph, starting at the initial node and following the current best path, and accumulate the set of nodes that are on that path and have not yet been expanded or labeled as SOLVED.

(b) Pick one of these unexpanded nodes and expand it. If there are no successors, assign FUTILITY as the value of this node. Otherwise, add its successors to the graph and for each of them compute f’. If f' of any node is o, mark that node as SOLVED.

(c) Change the f' estimate of the newly expanded node to reflect the new information provided by its successors. Propagate this change backward through the graph. If any node contains a successor arc whose descendants are all solved, label the node itself as SOLVED.

At each node that is visited while going up the graph, decide which of its successor arcs is the most promising and mark it as part of the current best path. This may cause the current best path to change. This propagation of revised cost estimates back up the tree was not necessary in the best-first search algorithm because only unexpanded nodes were examined. But now expanded nodes must be re-examined so that the best current path can be selected. Thus it is important that their f’ estimates should be the best available estimates.

29. Write the steps of the Constraint Satisfaction algorithm.

Q29.Answer

Constraint satisfaction

Artificial Intelligence Question Bank with Answers: part 1 link click here

Artificial Intelligence Question Bank with Answers: part 2 link click here